| |
Олимпиады по информатике проводятся ежегодно: в декабре –
районные, а в январе - областные. Для успешного участия в них от
учащихся требуется: максимум усилия при решении задач, высокий
уровень знания языка программирования, операционной системы и
обращения с компьютером. Чтобы добиться всего этого, должна
происходить длительная подготовка, а главное - самоподготовка
учащихся.
В СОШ пос. Маяк подготовка к олимпиадам по
информатике проводится в предметном кружке «Юный программист».
Обучение в кружке планируется на год: с января по май - первая
половина и с сентября по декабрь - вторая половина. Методика
обучения в кружке (групповая, индивидуальная и др.) выбирается в
зависимости от уровня знания учащихся и углубленности изученного
материала. В предметный кружок привлекаются одарённые дети с
6-го и выше классов. Разновозрастность учащихся создает
определённые трудности для освоения нового материала, но с
другой стороны она необходима для передачи накопленного опыта.
Годовой материал обучения в кружке в основном остаётся
неизменным, исключение составляют те материалы, в которых
отражаются требования к задачам и их оформлению. Например, из
опыта последних десяти лет можно заключить то, что предложенные
задачи на олимпиадах становятся всё сложнее, разнообразнее,
более математические и требуют глубокие знания компьютерной
техники.
Тематическое планирование обучения учащихся в кружке было
составлено из требований олимпиад, а также из тех тем, которые
требуют большое время практических занятий на компьютере.
Тематическое планирование обучения в кружке «Юный программист»
на 2001-2002 учебный год приведёно в приложении.
Успешное завершение годового обучения в кружке и
самоподготовка даст нашим ученикам более достойно выступить в
предстоящих олимпиадах по информатике.
Данная работа представляет практический интерес для учителей
информатики и учеников старших классов, увлекающихся
компьютерами. Основываясь на ней, педагог поможет овладеть
необходимым объёмом знаний его воспитанникам для участия в
олимпиадах. |
Раздел 1
Задачи с решениями районной олимпиады по информатике в 2001/2002
учебном году
1.1.1 ЗАДАЧА 1 :
Вводится натуральное число N и два вещественных числа А1 и А2.
Найти значение N –ого элемента последовательности {Aк},
определенной следующим образом : при нечетном к > 2 Ак равен
среднему арифметическому всех предшествующих элементов
последовательности с четными номерами, при четном к > 2 Ак равен
среднему арифметическому всех предшествующих элементов
последовательности с нечетными номерами . Оценка 20 баллов .
Технические
требования .
Входными данными являются натуральное число N (N <= 200000) и
два вещественных числа А1 и А2 , отделенные друг от друга
символами « пробел» или «перевод строки» .
Выходные данные – вещественное число с тремя цифрами после
десятичной точки, представляющее собой результат работы
программы.
Время работы программы - 15 сек.
Пример входных данных INPUT1.TXT
4 5 6
Пример выходных данных (для приведённых выше входных данных )
OUTPUT1.TXT
5.500
1.1.2
Алгоритм решения задачи :
Построим последовательность Ак:
А1
А2
А3 = А2
А4 = (А3 + А1)/2
А5 = (А4 + А2)/2
А6 = (А5 + А3 +А1)/3 = (2А4 + А5)/3
А7 = (А6 + А4 +А2)/3 = (2А5 + А6)/3
А8 = (А7 + А5 + А3 + А1)/4 = (3А6 + А7)/4
А9 = (А8 + А6 + А4 + А2)/4 = (3А7 + А8)/4
А10= (А9 + А7 + А5 + А3 + А1)/5 = (4А8 + А9)/5
А11= (А10 + А8 + А6 + А4 + А2)/5 = (4А9 + А10)/5
…………………………………………………….
___________________ Общая формула : Ак= (([k/2]-1)*Ak-2 +
Ak-1)/[k/2]
Из общей формулы видно, что для вычисления любого члена
последовательности нужно знать всего два предыдущих члена.
Описание алгоритма :
-
Ввод значений переменных
из файла INPUT1.TXT ;
-
А1 и А2 - первые два члена
последовательности ; n - номер требуемого члена
последовательности.
-
Вычисление 4 – ого члена
последовательности : к1 = (А1 + А2)/2;
-
Вычисление 5 – ого члена
последовательности : к2 = (А2 + к1)/2;
-
Цикл
: I = 6 ... n ;
-
Вычисление целой части
числа : к3 = [I / 2];
-
Вычисление следующего
члена последовательности : к4 = ((к3 – 1)* к1 + к2)/ к3;
-
Cохранения последних двух
членов последовательности в ячейках к1 и к2 : к1 = к2 ,
к2 = к4;
-
Конец цикла ;
-
Запись результата к4 в
файл OUTPUT1.TXT;
-
Конец программы.
|
1.1.3 Блок – схема решения задачи :
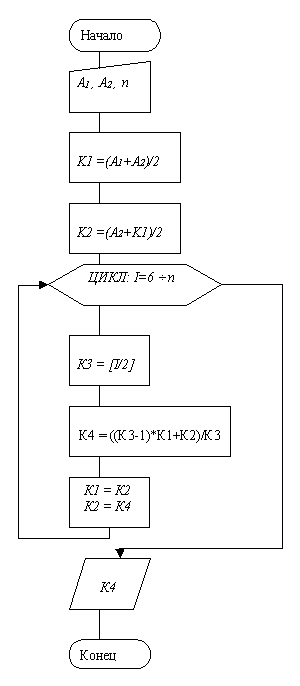
|
1.1.4 Программа на языке TURBO
PASCAL :
Program A1;
Uses crt;
Const n=3;
k5='isx_dan.pas';
k6='rez_dan.pas';
Var r:array[1..N] of integer;
INPUT1,OUTPUT1:TEXT;
i,k3:integer; a1,a2,k1,k2,k4:real;
begin clrscr;textcolor(11);
assign(INPUT1,k5);reset(INPUT1);
for i:=1 to n do read(INPUT1,R[i]);
close(INPUT1);
k1:=(R[2]+R[3])/2;
k2:=(R[3]+k1)/2;
for i:=6 to R[1] do begin
k3:=i div 2;
k4:=((k3-1)*k1+k2)/k3;
k1:=k2;k2:=k4;
end;
writeln('rezultat=',k4:10:4);
READLN;
assign(OUTPUT1,K6);
REWRITE(OUTPUT1);
WRITELN(OUTPUT1,K4);
CLOSE(OUTPUT1);END.
|
1.2.1
Задача 2:
Вводится число N и затем цифры N-значного числа. Найти все
натуральные делители числа, не превосходящие 12.
Технические
требования.
Входными данными являются натуральное число N(N<=1000000),
расположенное в первой строке входного файла и начиная со второй
строки, N десятичных цифр отделённые друг от друга символами
«пробел» или «перевод строки».
Выходные данные – натуральные числа, представляющие собой
результат работы программы, отделенные друг от друга пробелами.
Время работы программы – 15 сек.
Пример входных данных INPUT2.TXT
2
12
Пример выходных данных (для приведённых выше входных данных)
OUTPUT2.TXT
1 2 3 4 6 12
1.2.2 Алгоритм решения задачи:
В алгоритме используются следующие правила делимости:
-
на 2: если последняя цифра
числа делится на 2;
-
на 3: если сумма цифр
числа делится на 3;
-
на 4: если число,
состоящее из последних двух цифр числа, делится на 4;
-
на 5: если последняя цифра
числа «0» или «5»;
-
на 6: если одновременно
выполняются правила делимости на 2 и на 3;
-
на 7: умножить первую
слева цифру числа на 3 и прибавить следующую цифру;
результат умножить на 3 и прибавить следующую цифру и
т.д. до последней цифры числа. Если окончательный
результат делится на 7, то и данное число делится на 7;
-
на 8: если число,
состоящее из последних трёх цифр числа, делится на 8;
-
на 9: если сумма цифр
числа делится на 9;
-
на 10: если последняя
цифра числа «0»;
-
на 11: если сумма цифр
числа через одну равна сумме остальных цифр через одну
или разность этих сумм делится на 11, то и данное число
делится на 11;
-
на 12:
если одновременно выполняется правила делимости на 3 и
на 4.
Описания алгоритма:
1. Ввод значений переменных из файла INPUT2.TXT;
- N – длина числа;
- А1 … Аn – цифры числа.
2.Проверка на делимость на 2, 3,…,12;
3.Запись всех делителей на файл OUTPUT2.TXT;
4.Конец программы.
|
1.2.3 Блок – схема решения задачи:
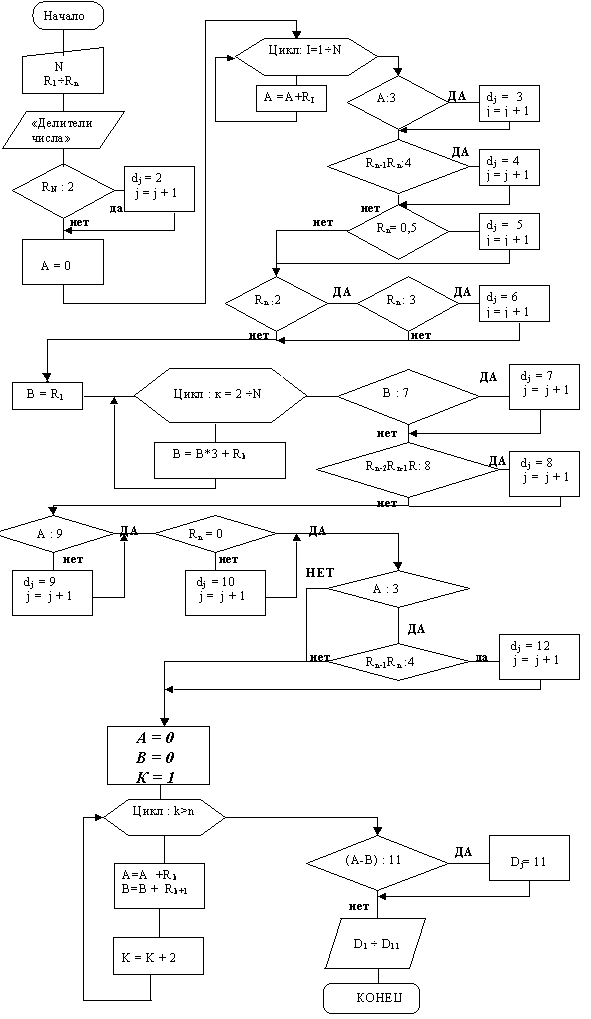 |
|
1.2.4
Программа
на
языке
TURBO PASCAL :
PROGRAM A38;
USES CRT;
const k1='isx_dan.pas';
k2='rez_dan.pas';
var r:array[1..100] of integer;
d:array[1..11] of integer;
input2,output2:text;
a,b,i,k,j,n:integer;
begin clrscr;textcolor(9);
assign(input2,k1);
reset(input2); readln(input2,n);
for i:=1 to n do read(input2,r[i]);
close(input2);
writeln('DLINA CHISLA:',n:5);
write('Chislo:'); j:=1;
for i:=1 to n do write(r[i]:2);
IF (r[n] mod 2)=0 then begin d[j]:=2; j:=j+1;end;
a:=0; for k:=1 to n do a:=a+r[k];
if (a mod 3)=0 then begin d[j]:=3;j:=j+1;end;
if ((10*r[n-1]+r[n]) mod 4)=0 then begin d[j]:=4;j:=j+1;end;
if (r[n]=0) or (r[n]=5) then
begin d[j]:=5;j:=j+1;end;
if ((a mod 3)=0) and ((r[n] mod 2)=0) then begin
d[j]:=6;j:=j+1;end;
b:=0;for k:=1 to n do b:=b*3+r[k];
write(b:5);
if (b mod 7)=0 then begin d[j]:=7;j:=j+1;end;
if (r[n]+10*r[n-1]+100*r[n-2]) mod 8=0 then begin
d[j]:=8;j:=j+1;end;
if (a mod 9)=0 then begin d[j]:=9;j:=j+1;end;
if (r[n]=0) then begin d[j]:=10;j:=j+1;end;
if ((a mod 3)=0) and (((r[n]+10*r[n-1]) mod 4)=0) then begin
d[j]:=12;j:=j+1;end;
a:=0;b:=0;k:=1;repeat
a:=a+r[k];b:=b+r[k+1]; k:=k+2;
until k>n;
if ((a-b) mod 11)=0 then d[j]:=11;
Writeln; Write('Deliteli :');
for i:=1 to 11 do write(d[i]:3);
assign(output2,k2);
rewrite(output2); Write(output2,'Deliteli :');
for i:=1 to 11 do write(output2,d[i]:3);
close(output2);readln
end. |
1.3.1
Задача 3:
Вводится:
- число N;
- координаты N вершин многоугольника, расположенного на
координатной плоскости, в порядке их обхода против часовой
стрелки;
- координаты двух точек плоскости.
Определить, будет ли прямая, проходящая через последние две
заданные точки, пересекать границу многоугольника хотя бы в
одной точки.
Технические
требования.
Входными данными являются натуральное число
N(2<N<21),расположенное в первой строке входного файла, и
,начиная со второй строки,2N+4,чисел,отделенного друг от друга
символами «пробел» или «перевод строки».Пара чисел с номерами
2i,2i+1 представляют собой координаты I-той вершины
многоугольника (I=1,2…,N).Последние 4числа-координаты двух
произвольных точек плоскости.>
Выходные данные – одно слово «да» или «нет» ,представляющее
собой результат работы программы.
Время работы программы-15 секунд. Пример входных данных
INPUT3.TXT
3
0 0
0 2
2 0
3 3
3 0
Пример выходных данных ( для приведенных выше входных данных)
OUTPUT3.TXT
НЕТ
1.3.2 Алгоритм решения задачи.
Координаты вершин многоугольника даны по порядку и поэтому
каждую сторону многоугольника можно принять как линию,
проходящую через две последовательные вершины. Например, сторона
соединяющих вершин (X1,Y1) и (X2,Y2) отражается уравнением
(X-X1)/(X2-Х1)=(Y-Y1)/(Y2-Y1 )
или Ax + By = C,
где A = 1 / (X2-X1 ),
B = 1 / (Y1-Y2) ,
C = X1 / (X2-X1) - Y1 / (Y2-Y1).
Таким образом , многоугольник превратится в семейство прямых
отрезков и надо решать пересекаются ли хотя бы одна из них с
заданной линией на плоскости, т.е. надо решить следующую систему
уравнения:
А1х + В1у = С1
А2х + В2у = С2
D = A1*B2 – A2*B1 ;
Dx = C1*B2 - C2 *B1 ;
Dy = A1*C2 - A2*C1 ;
Если D <> 0, то х = Dx / D ; y = Dy / D.
Точка (х , у) является точкой пересечения линии с
многоугольником.
Описания алгоритма:
- Ввод значений переменных из файла INPUT3.TXT
- n - количество вершин ;
- x1 y1 , … , x n y n - координаты вершин
многоугольника ;
- x1 y1, x2 y2 - координаты двух точек плоскости .
-
Вычисления коэффициентов
прямой проходящей через заданные две точки плоскости : A2,
B2 и C2 -------> A2 х+ В2у =С2
-
Цикл:
I = 1... n;
-
Вычисления коэффициентов
прямой, проходящей через две вершины многоугольника: A1, B1
и C1 ---------> A1х + B1у = С1
-
Решение системы уравнений: А1х
+ В1у = С1 A2 х + В2у = С2
-
Проверка : находится ли точка
пересечения этих линий на стороне многоугольника; если да ,
то l = 2;
-
Конец цикла.
-
Проверка : l = 2 ? если да, то
ОТВЕТ = «да», иначе ОТВЕТ = «нет»;
-
Запись значения ответа на файл
OUTPUT3.TXT;
-
Конец
программы.
|
|
1.3.3 Блок – схема решения задачи:
 |
Программа на языке TURBO PASCAL :
Program A39;
Uses crt;
Const k1='ISX_DAN.PAS';
K2='REZ_DAN.PAS';
Var x,y:array[1..10] of integer;
r:array[1..20] of integer;
input3,output3:text;
x1,y1,x2,y2,l,i,n:integer;
x0,y0,a1,b1,c1,a2,b2,c2,d,d1,d2:real;
begin clrscr;textcolor(10);
assign(input3,k1);reset(input3);readln(input3,n);
for i:=1 to n do readln(input3,x[i],y[i]);
readln(input3,x1,y1); readln(input3,x2,y2);
close(input3); l:=1; x[n+1]:=x[1]; y[n+1]:=y[1];
a2:=1/(x2-x1);b2:=1/(y1-y2);
c2:=x1/(x2-x1)-y1/(y2-y1);
for i:=1 to n do begin
a1:=1/(x[i+1]-x[i]); b1:=1/(y[i]-y[i+1]);
c1:=x[i]/(x[i+1]-x[i])-y[i]/(y[i+1]-y[i]);
d:=a1*b2-a2*b1;
d1:=c1*b2-c2*b1;
d2:=a1*c2-a2*c1;
if d<>0 then begin
x0:=d1/d; y0:=d2/d;
if ((x0<=x[i]) and (x0>=x[i+1])) or
((x0>=x[i]) and (x0<=x[i+1])) then
if ((y0>=y[i]) and (y0<=y[i+1])) or
((y0>=y[i]) and (y0<=y[i+1])) then l:=2;
end else if(d1=0) and (d2=0) then l:=2;end;
if l=2 then write('Otvet:da!')
else write('Otvet:net!');
assign(output3,k2);
rewrite(output3);
if l=2 then write(output3,'DA!')
else write(output3,'NET!');
close(output3); readln end. |
| |
|
Раздел 2
Задачи с решениями областной олимпиады по информатике в
2001/2002 учебном году
2.1.1 Задача 1
«Ломаная » (35 баллов):
Маленький мальчик взял листок бумаги в клетку размером N*N
клеток и нарисовал на нём замкнутую М-звенную ломаную с
вершинами в узлах клеток. После этого он выписал квадраты длин
звеньев ломаной в порядке их обхода по ломаной, а затем выкинул
свой рисунок. Необходимо определить существует ли хотя бы одна
ломаная соответствующая записанным мальчиком данным, или он
ошибся в подсчёте расстояний. Если такая ломаная существует, то
нужно её воспроизвести.
Требуется написать программу, которая определяла бы возможность
восстановления ломаной по заданной последовательности квадратов
длин её звеньев, и в случае положительного ответа вычисляла
координаты всех вершин ломаной.
Технические требования :
Входной файл : INPUT.TXT
Выходной файл : OUTPUT.TXT
Ограничение по времени тестирования : 5 секунд на один тест.
Формат входных данных :
Входной файл INPUT.TXT состоит из двух строк. В первой строке
содержатся два целых числа :
- N -размер бумаги в клетку (1 <= N<= 15) ;
- М -количество звеньев в ломаной ( 3 <= М <= 20 ).
Вторая строка содержит последовательность из М целых чисел ,
являющихся . квадратами длин звеньев ломаной .
Формат выходных данных :
В случае наличия решения данной задачи выходной файл OUTPUT.TXT
должен состоять из М строк, в I-ой строке которого содержатся
координаты вершин ломаной Хi и Yi , где Xi , Yi - целые числа и
0 <= Xi <= N , 0 <= Yi <= N . Порядок записи координат вершин
ломаной в строках должен соответствовать порядку записи
квадратов длин звеньев ломаной во входном файле .
В случае наличия нескольких решений следует найти хотя бы одно
из них . Если по исходным данным ломаную восстановить не
возможно , то выходной файл должен содержать сообщение : “Нет
решения “.
Пример файлов входных и выходных данных :
INPUT.TXT
8 4
13 29 37 5
OUTPUT.TXT
0 1
3 3
8 1
2 0
INPUT.TXT
8 4
1 1 1 2
OUTPUT.TXT
Нет решения
2.1.2 Алгоритм решения задачи:
По условию задачи вершины многоугольника находятся в узлах
клеток, т.е. координаты вершин целые числа. Нам даны квадраты
длин звеньев ломаной и по теореме Пифагора можно вычислить
проекции каждого звена на осях координат, например:
Даны : 13 , 29 ,37 , 5
13 = 9 + 4 = 32 + 22 (3,2) или (2,3) , …
29 = 25 + 4 = 52 + 22 (5,2) или (2,5) , …
37 = 36 + 1 = 62 + 12 (6,1) или (1,6) , …
5 = 4 + 1 = 22 + 12 (2,1) или (1,2) , …
Значения проекций могут быть в 8 – и разных вариантах, например:
Х = 3 , 2 , -3 , 3 , -2 , 2 , -3 , -2 .
У = 2 , 3 , 2 , -2, 3 , -3 , -2 , -3 .
Наша цель - используя эти проекции восстановить многоугольник
так, чтобы все полученные звенья многоугольника лежали бы на
бумаге. Для этого заполняем двумерный массив по правилам :
- количество строк соответствует количеству звеньев ;
- в каждой строке 16 проекций ( 8 пар (хi ,уi)).
Заполним двумерный
массив для нашего примера :
13 -------> 3 2 2 3 -3 2 3 -2 -2 3 2 -3 -3 -2 -2 -3
29 -------> 5 2 2 5 -5 2 5 -2 -2 5 2 -5 -2 -5 -5 -2
37 -------> 6 1 1 6 -6 1 6 -1 -1 6 1 -6 -6 -1 -1 -6
5 --------> 2 1 1 2 -2 1 2 -1 -1 2 1 -2 -2 -1 -1 -2
Первой точкой многоугольника может быть любая точка на бумаге.
Если для выбранной начальной точки сумма проекций по X-y и по
Y-y равны нулю и при этом , ни одно звено ломаной, ни вышло за
бумагу, то полученные координаты точек будут вершинами
многоугольника. Если , использовав все точки бумаги ,не найдём
решения, то ответом будет выражение: « НЕТ решения».
Описание алгоритма:
- Ввод значений переменных из файла INPUT . TXT:
-N-размер бумаги (N*N);
-M-количество сторон многоугольника;
-R[1÷M] – квадраты длин звеньев ломаной.
-
Вычисления проекций по
координатным осям каждого звена ломаной.
-
Заполнение двумерного массива
P[i ,j] значениями проекций звеньев ломаной;
-
Распечатка (вывод на монитор)
двумерного массива P[i,j] ;
-
Цикл: к1,к2,к3,к4= 1÷ 8;
-
Вычисление суммы проекций
звеньев ломаной ;
-
Проверка : ΣХi = 0 и ΣYi = 0
;
-
Если да, то вычисления
координат вершин многоугольника;
-
Проверка: координаты вершин
находятся ли на бумаге;
-
Если да, то l=1;
-
Конец цикла;
-
Если l╪1,то вывод «Нет
решения!»;
-
Если l=1,то вывод на монитор
координат вершин многоугольника.
-
Запись координат полученных
точек на файл OUTPUT.TXT;
-
Конец программы.
|
|
2.1.3 Блок – схема
решения задачи:

|
2.1.4
Программа
на
языке
TURBO PASCAL :
program b1;
uses crt;
const k5='ISX_DAN.PAS'; k6='REZ_DAN.PAS';
label v1,v2;
Var INPUT1,OUTPUT1: text;
r,d,X,Y :array[1..10] of integer;
P :array[1..10,1..16] of INTEGER;
n,m,i,j,k,l,a,b,x0,y0,k1,k2,k3,k4 :integer;
c :real;
begin clrscr; textcolor(11);
assign(INPUT1,k5); assign(OUTPUT1,k6);
reset(INPUT1); rewrite(OUTPUT1);
readln(INPUT1,n,m);
for i:=1 to m do read(INPUT1,r[i]);
close(INPUT1);k:=1; for i:=1 to 10 do d[i]:=i*i;
for i:=1 to m do begin l:=1;
for j:=1 to 10 do if r[i]>d[j] then if l=1 then
begin c:=sqrt(r[i]-d[j]);
if frac(c)=0 then begin x[k]:=round(c);
y[k]:=j; l:=2; k:=k+1; end; end; end;
for k:=1 to m do begin a:=x[k]; b:=y[k];
p[k,1]:=a;p[k,2]:=b;p[k,3]:=b;p[k,4]:=a;
p[k,5]:=-a;p[k,6]:=b;p[k,7]:=a;p[k,8]:=-b;
p[k,9]:=-b;p[k,10]:=a;p[k,11]:=b;p[k,12]:=-a;
p[k,13]:=-a;p[k,14]:=-b;p[k,15]:=-b;p[k,16]:=-a; end;
for i:=1 to m do begin
for j:=1 to 16 do begin write(p[i,j]:3);end; writeln; end;
for k1:=1 to 16 do for k2:=1 to 16 do
for k3:=1 to 16 do for k4:=1 to 16 do
begin x0:=p[1,k1]+p[2,k2]+p[3,k3]+p[4,k4];
y0:=p[1,k1+1]+p[2,k2+1]+p[3,k3+1]+p[4,k4+1];
if (x0=0)and(y0=0) then for i:=0 to n do
for j:=0 to n do begin x[1]:=i; y[1]:=0;
x[2]:=x[1]+p[1,k1];y[2]:=y[1]+p[1,k1+1];
x[3]:=x[2]+p[2,k2];y[3]:=y[2]+p[2,k2+1];
x[4]:=x[3]+p[3,k3];y[4]:=y[3]+p[3,k3+1]; l:=1;
for i:=1 to m do if (x[i]>n)or(x[i]<0) or(y[i]>n)or(y[i]<0)
then l:=2;
if l=1 then goto v1;end;end; writeln('HET PESHEHIJA !');
WRITE(OUTPUT1,'HET PESHEHIJA !');GOTO V2;
v1: Writeln('Bepshini :'); for i:=1 to m do
writeln(x[i]:3,y[i]:3); for i:=1 to m do
writeln(OUTPUT1,x[i]:3,y[i]:3);
v2: close(OUTPUT1); readln end.
|
2.2.1
Задача
2.
«Новобранцы» (20 баллов)
На первом построении вновь призванные в армию солдаты
построились в шеренгу. После небольшого объяснения им правил
выполнения в строю различных команд последовала команда
«налево». В результате исполнения этой команды некоторые солдаты
повернулись на лево, а некоторые - направо. Солдаты, которые
оказались лицом к лицу со своим соседом, сразу поняли, что
совершили ошибку. Чтобы ее исправить, каждый из них опять быстро
повернулись на 180 градусов. Если названия ситуация затем опять
повторилась, то есть, в каких – то парах солдаты оказывались
лицом друг к другу, то солдаты снова поворачивались на 180
градусов. Эта процедура продолжалась до тех пор, пока в шеренге
была хотя бы одна пара солдат, стоящих лицом друг к другу.
Требуется написать программу, которая по расположению солдат
сразу после исполнения команды «налево» вычисляет число пар
солдат, совершивших в последствии разворота на 180 градусов в
соответствии с выше описанной процедурой.
Технические требования:
Входной файл: INPUT.TXT
Выходной файл: OUTPUT.TXT
Ограничение по времени тестирования:5 секунд на один тест.
Формат входных данных:
Входной файл INPUT.TXT состоит из двух строк. В первой строке
этого файла записано число N(1<= N <=30000) – количество солдат
в шеренге. Во второй строке содержится последовательность из N
символов, каждый из которых может быть либо символом <, либо
символом >(символ < означает солдата, повернувшегося на лево,
символ > - солдат, повернувшегося на право.) Формат выходных
данных:
Выходной файл OUTPUT.TXT должен содержать, либо одно число -
количество развернувшихся пар, либо слово NO , если процесс
бесконечен.
Пример файла входных данных:
6
>><<><
Пример файла выходных данных ( для приведённого выше входного
файла):
7
2.2.2--Алгоритм решения задачи :
Шеренгу солдат обозначим одномерным массивом состоящий из
символов «>» и «<». При встречи в массиве , подряд стоящих
символов «><» заменяем на «><>» и счётчик увеличиваем на один.
При обработки массива , если не произошла ни одна замена, то
работа программы завершается. Результатом обработки станет
количество замен.
Описание алгоритма:
- Ввод значений переменных из файла INPUT2.TXT:
- N – количество солдат в шеренге;
- <….>- последовательность N символов ;
- если R[I] = ‘>’ и R[i +1] = ‘<’, то
- присвоить: R[i] = ‘><’ и R[i+1] = ‘>’ ;
- счётчики: l = l + 1 ; I = I + 1;
- указатель: d = 0 - нет замены; d = 2 – есть замена;
- если d = 2 , то идти п.2;
- если d = 0 , то вывод результата на монитор;
- Запись результата файла OUTPUT2.TXT;
- Конец
программы.
|
|
2.2.3 Блок - схема решения задачи:

|
2.2.4
Программа
на
языке
TURBO PASCAL :
program b2;
uses crt;
const k1='ISX_DAN.PAS';
k2='REZ_DAN.PAS';
label v0,v1;
var R:array[1..100] of char;
INPUT2,OUTPUT2 :text;
n,l,d,i :integer;
begin clrscr;textcolor(11);
assign(INPUT2,k1);
reset(INPUT2);
readln(INPUT2,n);
for i:=1 to n do read(INPUT2,r[i]);
close(INPUT2);
l:=0;d:=0;i:=1;
v0: if r[i]='>' then if r[i+1]='<'
then begin d:=2;l:=l+1;r[i]:='<';r[i+1]:='>'; i:=i+1; End;
i:=i+1;
if i>N then begin i:=1;
if d=0 then goto V1;
d:=0;
End;
goto V0; V1:
Write('Pezultat=',l);
for i:=1 to N do Write(R[i],' ');
assign(OUTPUT2,K2);
rewrite(OUTPUT2);
Write(OUTPUT2,l);
Close(OUTPUT2);
readln
End.
|
2.3.1 Задача
3. «Театр» (20 баллов)
В театре N мест, пронумерованных целыми числами от 1 до N.
Некоторые из зрителей опоздали на спектакль, поэтому после
третьего звонка те зрители, которые имели билеты на неудобные
места, присели на более удобные. Опоздавшие зрители, которые
пришли уже после третьего звонка, садились на первое попавшееся
свободное место. В антракте один из опоздавших зрителей решил
сесть на своё место.
Если его место до этого было занято, то тот, кто там сидел,
пересаживался на своё место. Если и там кто-то уже сидел, то и
этот зритель также вынужден был вернуться на своё место. И так
далее.
Поскольку в театр попали только зрители, имевшие на руках
билеты, то начавшийся на антракте процесс пересаживания зрителей
обязательно заканчивался. Необходимо посчитать, сколько человек
в результате такого пересаживания были вынуждены поменять на
свои места.
Требуется написать программу, которая вычисляет количество
зрителей, поменявших свои места из-за опоздания одного зрителя.
Технические требования :
Входной файл : INPUT3.TXT
Выходной файл : OUTPUT3.TXT
Ограничение по времени тестирования : 5 секунд на один тест.
Формат входных данных :
Входной файл INPUT3.TXT состоит из трёх строк. В первой строке
содержится целое число N(N ? 30000) – количество мест в зале.
Вторая строка содержит последовательность из N целых чисел,
разделённых пробелами, где первое число определяет номер места в
билете у зрителя, который занял место с номером 1 , второе -
номер места в билете у зрителя , который занял место с номером 2
, и так далее. Если место было свободно ,то соответствующее
число равно 0 .
В третьей строке содержится одно число – номер листа в билете у
опоздавшего зрителя, который в антракте решил пересесть на свое
место.
Формат выходных данных:
Выходной файл OUTPUT3.TXT должен содержать одно число-количество
зрителей, поменявших свои места в антракте, включая опоздавшего
зрителя.
Пример файлов входных и выходных данных:
INPUT3.TXT 10 0 2 5 3 1 0 0 0 0 0 4 OUTPUT3.TXT 3 2.3.2 Алгоритм
решения задачи:
В зале N мест и зрители с билетами сидят по местам
R1,…,Rn;(R-одномерный массив).Для опоздавшего выделим место в Е
так, чтобы при смене мест опоздавший садится на свое место ,а
сидевший зритель перемещается на место опоздавшего. Теперь весь
процесс повторяем для него. Алгоритм завершается только тогда
,когда «опоздавший» зритель находит пустое место. Результатом
является количество зрителей, поменявших свои места.
Описание алгоритма:
1.Ввод значений переменных из файла INPUT3.TXT;
-N-количество мест в зале;
-R1…Rn-зрители с билетами;
-D-номер места в билете у опоздавшего зрителя.
2. Если есть «опоздавший», то 3,иначе 6;
3. «Опоздавший» меняется местами с сидящим зрителям, теперь
«опоздавшим» будет ранее сидящий зритель;
4. Счётчик: l=l+1;
5. Идти к 2 .
6. Вывод всех зрителей с билетами;
7. Запись на файл OUTPUT.TXT числа - количество зрителей,
поменявших свои места;
8. Конец
|
|
2.3.3. Блок- схема решения задачи
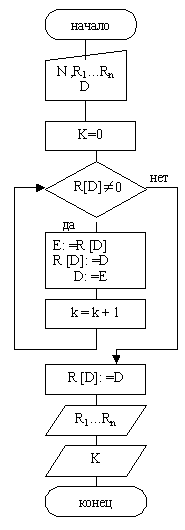
|
2.3.4
Программа
на
языке
TURBO PASCAL:
Program B3;
Uses CRT;
Const K1='ISX_DAN.PAS';
K2='REZ_DAN.PAS'; Label V1;
Var R: array [1.100] Of integer;
Input3, Output3: text;
N, D, I, K, E: integer;
Begin clrscr; textcolor (11);
Assign (Input3, K1); reset (Input3);
readln (Input3, N);
For I: =1 to N does read (Input3, R [I]);
Writeln; readln (Input3, D);
For I: =1 to n does write(R [I]: 5);
Close (Input3); K: =0;
V1: if R [D]<>0 then begin E: =R [D]; R [D]: =D;
D: =E; K: =K+1;GOTO V1; End;
R [D]: =D; Writeln;
For I: =1 to N do Write(R [I]: 5);
Assign (Output3, K2); rewrite (Output3);
Write (Output3, K); Close (Output3);
Readln
End.
|
2.4.1
Задача
4. «Последовательность
чисел» (25 баллов)
Рассмотрим бесконечную в обе стороны последовательность целых
чисел Fi , в которой для любого целого I элемент Fi+2
вычисляется с использованием следующего условия Фибоначчи: Fi+2
= Fi+1+Fi.Пусть заданы две различных числа этой
последовательности - Fi и Fj с соответствующими номерами I и j,
а также некоторое целое число n.Необходимо восстановить элемент
этой последовательности Fn ,соответствующий номеру n.
Требуется написать программу, которая по заданным числам
I,Fi,j,Fj,n вычисляет искомый элемент Fn описанной выше
последовательности.
Технические требования:
Входной файл :INPUT4.TXT
Выходной файл: OUTPUT4.TXT
Ограничение по времени тестирования:5 секунд на один тест
Формат входных данных:
Входной файл INPUT4.TXT содержит в одной строке разделённые
пробелом следующие числа: I, Fi, j, Fj, n.Для этих чисел
справедливы следующие ограничения: -1000<=I,j, n<=1000;
-2000000000 <= Fk <= 2000000000 для всех к, удовлетворяющих
условию min(i,j,n) <= k <= max(i,j,n). Формат выходных данных:
Входной файл OUTPUT4.TXT должен содержать искомое число Fn.
Пример файлов входных и выходных данных: INPUT4.TXT
3 5 -1 4 5
OUTPUT4.TXT
12
2.4.2 Алгоритм решения задачи:
Для описания алгоритма сначала решим контрольный пример: Дано:
I, Fi, j, Fj, n; Найти: Fn =?
3 5 -1 4 5 F5 =? Последовательность целых чисел: … 5 4 3 2 1 0
-1 …
Введём новые переменные: а, в, с; … 5 а в с 4 …
По формуле Fi+2 = Fi+1 + Fi составим следующие уравнения :
5 = а + в
а = 2в - 4
а = в + с
5 = а + в
5 = 2в – 4 + в
3в = 9 , в = 3 ,а = 2 , с = -1
в = с + 4 Получим , N = 5 , 4 , 3 , 2 , 1 , 0 , -1
Fn = 12 , 7 , 5 , 2 , 3 , -4 , 4
Ответ : F5 = 12.
В данном примере между Fi и Fj три шага , их обозначим тремя
неизвестными : - а, в, с. Далее, с помощью формулы составим
систему трёх уравнений и решив её находим значения неизвестным.
Если расстояние между Fi и Fj увеличивается, то вычисления
неизвестных таким методом будет невозможным. Поэтому выбираем
другой - экспериментальный путь к решению задачи, т.е. задав
значения неизвестным, проверяем правильность выполнения формулы
в остальных точках. По условию задачи I u Fi целые числа, для
восстановления последовательности нужно знать два
последовательных значения, например: Fi u Fi+1 . В задаче
значение FI задано, а для Fi+1 выберем значение из интервала
целых чисел [-10,10] до тех пор, пока значения в точке Fj не
совпадут. При необходимости интервал можно расширить в два раза
и т.д.
Описания алгоритма :
1. Ввод значений переменных из файла INPUT4.TXT: - i - целое
число; - Fi - i -ый элемент последовательности;
- - j - целое число;
- - Fj- j -ый элемент последовательности;
- - n - целое число, для которого надо восстановить Fn.
2. Присвоить: к = 10;
3. Цикл: I = -k, k;
4. Продвижение от 2-ой контрольной точки к 1-ой, наращивая номер
элемента, вычисляется значения функции;
5. Если номер совпадает, то совпадает ли значение функции с
заданным;
6. Если да, то п.11, если нет то
7. Конец цикла.
8. Завершение цикла означает, что требуемого значения Fn в этом
интервале нет, и поэтому
9. Увеличиваем ширину интервала в 2 раза;
10. Идти к п.3;
11. Вычисление искомого значения Fn.
12. Вывод значения Fn на монитор и запись результата на файл
OUTPUT 4.TXT
13. Конец программы. |
2.4.3 Блок-схема решения задачи:
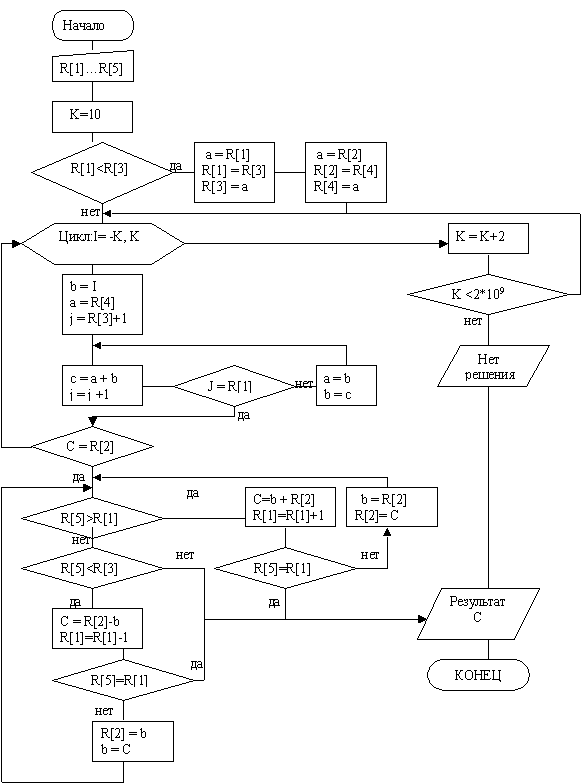
|
2.4.4 Программа на языке TURBO PASCAL :
Program B4;
Uses CRT;
Const K1='ISX_DAN.PAS';
K2='REZ_DAN.PAS';
label V0,V1,V2,V3,V4;
Var R:array[1..5] of longint;
INPUT4,OUTPUT4: text;
i,j,k,a,b,c :longint;
begin clrscr; textcolor(11);
assign(INPUT4,K1); reset(INPUT4);
for i:=1 to 5 do read(INPUT4,R[i]); close(INPUT4);
K:=10; if R[1] a:=R[1]; R[1]:=R[3]; R[3]:=a;
a:=R[2]; R[2]:=R[4]; R[4]:=a;end;
V0: for i:=-k to k do begin b:=i; a:=R[4]; j:=R[3]+1; V1:
c:=a+b;j:=j+1; if j=R[1] then
if c=R[2] then goto V3 else goto V2;
a:=b; b:=c; goto V1;
V2: End; K:=K*2; if K><200 then goto V0;
Write('Het pewenii!'); C:=0; goto V4;
V3 : if R[5]>R[1] then begin c:=b+R[2]; R[1]:=R[1]+1; if
R[5]=R[1] then goto V4;
b:=R[2]; R[2]:=c; goto V3; End;
if R[5] if
R[5]=R[1] then goto V4; R[2]:=b; b:=c; goto V3; End;
V4: Write('Pesyltat Fn=',c:3);
assign(OUTPUT4,K2); rewrite(OUTPUT4);
Write(OUTPUT4,c); close(OUTPUT4);
readln End. |
П Р И Л О Ж Е Н И
Я 1.
Тематическое планирование обучения учащихся в кружке « Юный программист
» Учебники:
- И .Семакин и др. «Базовый курс» учеб. 7-9 классы.
- Л .Залогова и др. «Задачник-практикум» 1,2 ч.
- Ю .Федоренко «Алгоритмы и программы на Turbo Pascal»
- А .Епанешников и др. «Программирование в среде Turbo Pascal 7.0»
| Дата
|
Тема уроков
|
Примечание |
| 14.01
|
Алгоритмы работы с величинами.
Линейные алгоритмы.
|
[2] cтр.204-206 задачи 6-10 |
| 21.01
|
Линейные алгоритмы на электронных таблицах.
Решения задач.
|
[2] стр. 220 задачи 27-38
|
| 28.01
|
Ветвление в алгоритме.
Решения задач на электронных таблицах.
|
[2] стр.206-210 задачи 12-23
|
| .02
|
Циклические алгоритмы.
Решения задач на электронных таблицах.
|
[2] стр. 207 задачи 24-41
|
| .02
|
Алгоритм Евклида.
Решения задач на Turbo Pascal.
|
[1] стр. 358 зад. 1-11 стр 361
|
| .02
|
Стандартные функции.
Программирования линейных алгоритмов на Turbo Pascal.
|
[2] стр. 213-219 задачи 1-26
|
| .03
|
Решения задач №27-55 на компьютере.
|
[2] стр.220-227
|
| .03
|
Программирования ветвящихся алгоритмов на Turbo Pascal.
|
[2] стр. 228-231 задачи 1-23
|
| .03
|
Решение задач №24-86 на компьютере.
|
[2] стр.231-240
|
| .04
|
Программирование циклических алгоритмов.
|
[2] стр.240-244 задачи 1-12
|
| .04
|
Решения задач №13-96 на компьютере.
|
[2] стр. 246-249
|
| .04
|
Решения сложных задач №97-137 на компьютере.
|
[2] стр. 250-254
|
| .05
|
Полиндромы. Решения задач №138-142 на компьютере.
|
[2] стр. 254
|
| .05
|
Одномерные массивы. Решения задач №1-19.
|
[2] стр. 255-258
|
| .05
|
Решения задач №20-49 на компьютере.
|
[2] стр. 259-264
|
| .09
|
Решения сложных задач №50-68 на компьютере.
|
[2] стр. 262-265
|
| .09
|
Двумерные массивы.
|
[2] стр. 265-267задачи 69-77
|
| .09
|
Решения задач №78-92 на компьютере.
|
[2] стр. 268-292
|
| .10
|
Решения сложных задач №93-125.
|
[2] cтр. 270-274
|
| .10
|
Подпрограммы: функции и процедуры.
|
[2] стр. 275-278задачи 1-8
|
| .10
|
Решения задач №9-19 на компьютере.
|
[2] стр. 279-280
|
| .11
|
Решения сложных задач №20-46 на компьютере.
|
[2] стр. 280-282
|
| .11
|
Рекурсивные подпрограммы, задачи 47-56.
|
[2] стр. 284-285
|
| .11
|
Обработка строк на языке Turbo Pascal, задачи 1-9.
|
[2] стр. 285-288
|
| .12
|
Решения задач №10-37 на компьютере.
|
[2] стр. 289-291
|
| .12
|
Решения сложных задач №38-61 на компьютере.
|
[2] стр. 291-293 |
2. Система двух линейных уравнений с двумя неизвестными
Общий вид системы:
а1*х + в1*у = с1
а2*х + в2*у = с2
|
Решим эту систему методом определителей.
D=
а1
b 1 Dх=
c1 b1 Dy = a1 c1
а2
b2 c2 b2 a2 с2
D = a1*b2 – a2*b1;
Dx= c1*b2 – c2*b1;
Dy= a1*c2 – a2*c1;
Если
D <> 0, то
X = Dx/D и
Y = Dy/D .
Если D = 0 и
a1/a2 = b1/b2 = c1/c2 , то система уравнений имеет бесконечное
множество решений.
Если D = 0 и а1/а2 <> в1/в2 или а1/а2 <> с1/с2 или в1/в2 <>
с1/с2 , то система уравнений не имеет решения.
|
Описание алгоритма :
1. Ввод значений коэффициентов :а1 , в1 , с1 , а2 , в2 , с2 ;
2. Вычисление: D = a1*b2 – a2* b1 ;
3. Вычисление: Dx= c1*b2 - c2* b1 ;
4. Вычисление: Dy = a1*c2 - a2*c1 ;
5. Если D<> 0 , то x = Dx/D и y = Dy/D;
6. Если D = 0 , Dx = 0 и Dy = 0 , то у системы бесконечное
множество решений ;
7. Если D = 0 , и DX<> 0 или Dу <> 0, то y системы нет решения.
8. конец. |
Программа на языке Turbo Pascal :
Program B1;
Uses crt;
Var a1,a2,b1,b2,c1,c2,d,dx,dy,x,y : real;
Begin clrscr; textcolor(10);
Writeln(‘Введите коэффициенты системы :);
Readln(a1,b1,c1,a2,b2,c2);
D:=a1*b2-a2*b1;
Dx=c1*b2-c2*b1;
Dy=a1*c2-a2*c1;
If D<>0 then begin
x:=Dx/D; y:=Dy/D; Write(‘x=’,x:6:3,’ y=’,y:6:3); End
else If (Dx = 0) and (Dy = 0) then
Write(‘ Система имеет бесконечное множество решений!’)
Else Write(‘ Система не имеет решения!’) End.
|
3. Система трёх линейных уравнений с тремя неизвестными :
1 Общий вид системы уравнений :
a1*х + b1*у + с1*z = d1
a2*x + b2*y + c2*z = d2
a3*x + b3*y + c3*z = d3
|
Методом определителей система уравнений решается следующем
образом :
D = a1b2c3 + a2b3c1 + a3b1c2 – a3b2c1 – a1b3c2 – a2b1c3 ;
Dx= d1b2c3 + d2b3c1 + d3b1c2 – d3b2c1 – d1b3c2 – d2b1c3 ;
Dy= a1d2c3 + a2d3c1 + a3d 1c2 – a3d 2c1 – a1d 3c2 – a2d 1c3 ;
Dz= a1b2d3 + a2b3d1 + a3b1d2 – a3b2d1 – a1b3d2 – a2b1d3
Если D<> 0 , то x = Dx/D , y = Dy/D , z = Dz/D .
Если D = 0 и Dx = 0 и Dy = 0 и Dz = 0 , то система уравнений
имеет бесконечное множество решений.
Если D = 0 и Dx <> 0 или Dy <> 0 или Dz <> 0 , то система
уравнений не имеет решения.
|
Описание алгоритма :
1. Ввод значений коэффициентов a1, b1, c1, d1, a2, b2, c2, d2,
a3, b3, c3, d3;
2. Вычисление D ;
3. Вычисление Dx ;
4. Вычисление Dy ;
5. Вычисление Dz ;
6. Если D<> 0 , то x =Dx/D , y =Dy/D , z = Dz/D ;
7. Если D = 0 и Dx = 0 и Dy = 0 и Dz = 0 ,
то вывод сообщения «Система имеет бесконечное множество решений
» ;
8. Если D = 0 и Dx <> 0 или Dy <> 0 или Dz <> 0 , то вывод
сообщения «Система не имеет решения.»;
9. Конец.
|
Программа на языке Turbo Pascal :
Program B21;
Uses crt;
Var a1, b1, c1, d1, a2, b2, c2, d2, a3, b3, c3, d3, D, DX, DY,
DZ, x, y, z :real;
begin clrscr; textcolor(11);
Writeln(‘Введите коэффициенты системы : ‘);
Readln(a1,b1,c1,d1,a2,b2,c2,d2,a3,b3,c3,d3);
D:=a1*b2*c3+a2*b3*c1+a3*b1*c2-a3*b2*c1-a1*b3*c2–a2*b1*c3 ;
Dx:=d1*b2*c3+d2*b3*c1+d3*b1*c2-d3*b2*c1-d1*b3*c2–d2*b1*c3 ;
Dy:=a1*d2*c3+a2*d3*c1+a3*d1*c2-a3*d2*c1-a1*d3*c2–a2*d1*c3 ;
Dz:=a1*b2*d3+a2*b3*d1+a3*b1*d2-a3*b2*d1-a1*b3*d2–a2*b1*d3 ;
If D<>0 then begin x:=Dx/D; y:=Dy/D; z:=Dz/D;
Write(‘ Ответ : х =’,x:6:3, ‘ y =’, y:6:3, ‘ z= ‘,z:6:3); end
else if (Dx=0) and (Dy=0) and (Dz=0) then
Write(‘Ответ : Система имеет бесконечное множество решений.’)
else write(‘Ответ : Система не имеет решения.’) End.
|
Л и т е р а т у р а
1. Х. Хасагава «Мир компьютеров». Москва. Мир. 1988 г
2. Тадао Отани «Компьютеры». Баку. Азернешр. 1987 г.
3. Статьи в журналах: «Информатика и образование», «Техника
молодёжи», «Микропроцессорные средства и системы»
4. Ю. Федоренко «Алгоритмы и программы на TURBO PASCAL»
5. А. М. Епанешников и др. «Программирование в среде TURBO PASCAL
7.0» 6.Учебники:
- Ю. Шафрин «Информационные технологии» в 2 ч. М. 2000 г.
- Залогова Л.А. и др. «Задачник – практикум» в 2т. М. 1999 г.
- И. Семакин и др. «Базовый курс». 7-9 класс. М. 2000 г.
- А. Г. Гейн и др. «Информатика». 7-9 классы. М. Дрофа.1998 г.
 Главное Главное |

