ГОТОВИМСЯ  К  ЕГЭ В начало

                                                         

Двоичные числа

    Двоичные  числа обозначаются цифрами 0 и 1, один разряд, которого называется  один    бит.

Чтобы двоичных чисел отличить от десятичных их обозначают:           

                (1010011)2
Таблица (А 2А8А10А16)

А2

 А8 А10 А16
0000 0 0 0
0001 1 1 1
0010 2 2 2
0011 3 3 3
0100 4 4 4
0101 5 5 5
0110 6 6 6
0111 7 7 7
1000 10 8 8
1001 11 9 9
1010 12 10 A
1011 13 11 B
1100 14 12 C
1101 15 13 D
1110 16 14 E
1111 17 15 F
А2 - двоичная;

А8 - восьмеричная;

А10 - десятичная;

А16 - шестнадцатеричная.
Преобразование двоичных чисел А2  ==>   А10  перевод двоичных чисел в десятичную (10011101)2  ==>   А10                                 

 = 27 +  24  +  23  +  22  +  20  =

128 + 16 +8 + 4 + 1 = 157

 (10011101)2 = 157

 20 = 1                  ...          

21 = 2                

22 = 4                

23 = 8                 

24 = 16

25 = 32

26 = 64

27 = 128

28 = 256

29 = 512

210 = 1024    ... 

А10  ==>   А2  перевод десятичных чисел в двоичную 109  ==>    А2            

109 = (1101101)2        

 Проверка:

=  26+25+23+22+20 =

=  64 +32 +8 + 4 + 1 = 109
А2  ==>   А8 перевод двоичных чисел в восьмеричную ПРАВИЛА1:  Для перевода двоичного числа в восьмеричную, надо двоичного числа начиная с конца разбить в группы по три разряда и написать полученные числа из таблицы.

Например,  (10110101101)2 = А8

          (10   110   101   101)2 = (2655)8

  
А8   ==>  А2 перевод восьмеричных чисел в двоичную (2655)8 ==> А2 = ( 010   110   101   101)2 =  (10110101101)2
А2  ==>   А16 перевод двоичных чисел в шестнадцатеричную ПРАВИЛА2:  Для перевода двоичного числа в шестнадцатеричную, надо двоичного числа начиная с конца разбить в группы по четыре разряда и написать полученные числа из таблицы.

Например,  (101101011010111)2 = А16

     (101   1010     1101    0111)2 = (5AD7) 16
А16   ==>  А2  перевод шестнадцатеричных чисел в двоичную (1F3A)16 ==> А2 = (0001   1111   0011   1010)2 = (1111100111010)2
Перевод десятичного дробя в двоичную (0,15625)10==> А2 =  (0.00101)2

                          Проверка:

  

= 2-3  +   2-5 =

=0.125  +  0.03125 = 0.15625

 0,15625  *  2  =                0,3125=> 0

 0,3125  *  2  =                      0,625 => 0

 0,625  *  2  =                               1 ,25 => 1

 0,25  *  2 = 0,5 => 0

 0,5  *  2  =  1   => 1

 0

 2-1   =  0,5             

2-2   =  0,25           

2-3   =  0,125 

2-4 =  0,0625 

2-5 =  0,03125

2-6=  0,015625

2-7=  0,0078125

Перевод смещенных чисел в двоичную 23,25==>А2                        

23,25 = 23  + 0,25         

23 ==> А2  

        

23 = (10111)2  

0,25 ==> А2   

0.25  *  2 = 0.5 =>  0

0.5  *  2  =  1    =>  1

0,25 = (0.01)2     

23,25 = (10111.01)2

Арифметика двоичных чисел

Сложение

двоичных чисел

    

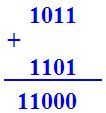 10112 => 11   11012 => 13   110002 => 24

                            11  +  13  =  24

Вычитание

двоичных чисел

  

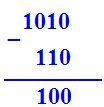  10102  => 10    1102 => 6    1002  =>  4

                        10  -  6  =  4

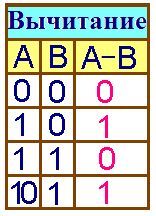Умножение

двоичных чисел

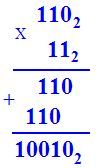 1102  => 6      112 =>  3     100102 => 18                        6  *  3  =  18

 

 

Деление

двоичных чисел

 1010102  =  25 + 23  + 21  = 42              

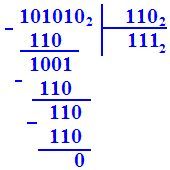110  =  6

111  =  7

42  :  6  =  7

 
Примеры: 1.Сколько единиц в двоичной записи числа 195?

Решение:

195 ==> A2                  195  =  (11000011)2           4 ед.  

 
2.Чему равна сумма чисел 438 и 5616?

Решение:

438 = 1000112                                        438  +  5616 =   1000112 +10101102  =                                                                   = 11110012 = 1718 =  7916

5616= 10101102                                                                                                                                                                                                                 

3.Дано а=D716, b=3318.

Какое из чисел c, записанных в двоичной системе,

отвечает условию a<c<b?

1. 11011001

2. 11011100

3. 11010111

4. 11011000

Решение:

а=D716 = 110101112                                      

b=3318 = 110110012

 a < c < b             

 11011001 >11011000 > 11010111   

                     Ответ: 4

 

 

В начало